Collisions in 1-D and 2-D

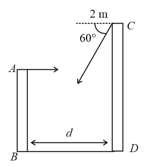
Two towers $AB$ and $CD$ are situated a distance $d$ apart as shown in figure. $AB$ is $20 \mathrm{m}$ high and $CD$ is $30 \mathrm{m}$ high from the ground. An object of mass $m$ is thrown from the top of $AB$ horizontally with a velocity of $10$ $\mathrm{m}{\mathrm{s}}^{-1}$  towards $CD$. Simultaneously another object of mass $2m$ is thrown from the top of $CD$ at an angle of $60°$ to the horizontal towards $AB$ with the same magnitude of initial velocity as that of the first object. The two objects move in the same vertical plane, collide in mid-air and stick to each other. Find the position where the objects hit the ground (from $B$).

A moving mass of $8 \mathrm{kg}$ collides elastically with a stationary mass of $2 \mathrm{kg}.$ If $E$be the initial kinetic energy of the moving mass, the kinetic energy left with it after the collision will be :-

Two identical balls each of mass $\mathrm{m}$ moving on straight track are approaching towards each other with same speed. Final kinetic energy of the two ball system is equal to the total energy loss during collision.$E$ is the total kinetic energy of the balls before collision and $E\text{'}$ is after collision and coefficient of restitution is $e$. Then choose the correct options

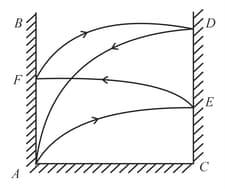
A particle is projected from the foot of one wall towards other parallel wall as shown in figure. After various collisions, finally after striking at point $D$ normally it comes back directly to the point of projection. If $e$ is the coefficient of restitution for each impact then $e^3+e^2+e$ is equal to

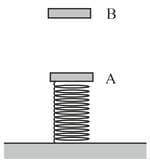
A thin plate $A$ of mass $m$ is affixed on the upper end of a spring, lower end of which is affixed on the ground. In equilibrium, the spring is compressed by an amount $x_0$. Another thin plate $B$ of mass $2m$ dropped from a height $3x_0$ above plate $A$ hits the plate $A$, moves downwards together with the plate $A$ and after reaching a lowest position, both the plates rebound upwards. What maximum height above the initial position of the plate $A$ will the plate $B$ rise?

​​​​​​​

A ball falls from a height such that it strikes the floor of lift at $10 \mathrm{m} {\mathrm{s}}^{-1}$. If lift is moving in the upward direction with a velocity $1 \mathrm{m} {\mathrm{s}}^{-1}$, then velocity with which the ball rebounds after elastic collision will be

A pendulum bob of mass $M$ is raised to height $h$ and released. At the bottom of its swing, it picks up a mass $m$. To what height will the combined mass rise?

An alpha particle collides elastically with a stationary nucleus and continues moving at an angle of $60°$ with respect to the original direction of motion.The nucleus recoils at an angle of $30°$ with respect to this direction. Mass number of this nucleus is

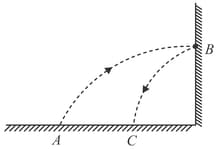
A ball is projected at an angle of $53°$ with a speed of $20 \mathrm{m} {\mathrm{s}}^{-1}$ towards a wall as shown in figure. Ball rebounds such that component of its velocity perpendicular to wall reverses without change in its magnitude while the component of its velocity parallel to the wall remains same. Consider no time lapse in collision. The average acceleration (in $\mathrm{m} {\mathrm{s}}^{-2}$) of the ball throughout the motion $\left(A\to B\to C\right)$ is $\left(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$

There is an elastic ball which is thrown towards a rigid wall. The work done by the normal reaction exerted by the wall on the ball is:

Board $A$ is placed on board $B$ as shown. Both boards slide, without moving with respect to each other, along a frictionless horizontal surface at a speed $6{\mathrm{ms}}^{-1}$. Board $B$ hits a resulting board $C$ "head-on". After the collision, board $B$ and $C$ stick together and board A slides on top of board $C$ and stops its motion relative to $C$ in the position shown on the diagram. What is the length (in $\mathrm{m}$) of each board?  AIl three boards have the same mass, size and shape. The coefficient of kinetic friction between boards $A$ and $C$ and between board $A$ and $B$ is $0.3$

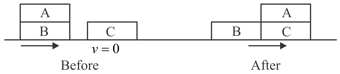
A bullet of mass $0.02 \mathrm{kg}$ is travelling with speed $100 \mathrm{m} {\mathrm{s}}^{-1}$ at an angle of $30°$ with respect to the horizontal. The bullet collides with and sticks to the end of a vertical thin rod of length $2.0 \mathrm{m}$ and mass $3 \mathrm{kg}$ as shown in the figure. The rod then rotates about its end which is hinged to the floor. Find (a) the angular velocity of the rod immediately after the collision and (b) the angular velocity of the rod just before when it hits the floor. Treat the bullet as a point mass.

​​​​​​​

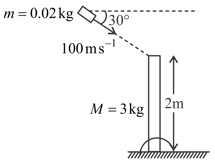
Particle $A$ is at rest and particle $B$ is moving with constant velocity $v$ as shown in diagram at $t=0$. Find their velocity of separation.

A sphere of mass $M$ moving with velocity $u$ collides head on elastically with a sphere of mass $m$ at rest. After collision their respective velocities are $V$ and $v$. The value of $V$:

For head-on collision between two colliding balls of equal radii $r$, the impact parameter is equal to

A particle of mass $m$ strikes another particle of same mass at rest elastically. After collision if velocity of one of the particle is $3\hat{i}-2\hat{j} \mathrm{m} {\mathrm{s}}^{-1}$, then the other must have a velocity equals to

Two identical masses are kept in contact on a smooth horizontal surface as shown. A third identical mass moving with speed $u$ hits the two balls symmetrically and comes to rest. The coefficient of restitution is

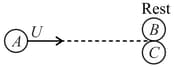
In a nuclear reactor, a neutron of high speed $\left(~{10}^7 \mathrm{m}{ \mathrm{s}}^{-1}\right)$ has to be slowed down to ${10}^3 \mathrm{m}{ \mathrm{s}}^{-1}$ so that it can have a high probability of interacting with the isotope ${}_{95}{}^{235}\mathrm{U}$ and cause it to fission. Show that fractional $KE$ transferred is about $90\%$ when a neutron has an elastic collision with a high nuclei of deuterium. (The material making up the light nuclei, usually heavy water $\left(D_2\mathrm{O}\right)$ or graphite, is called nuclei moderator).

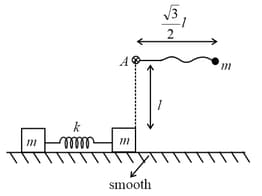
A simple pendulum of length $l$ and mass $m$ is hinged at point $A$ in a vertical plane as shown in the figure. The ball is released from the same horizontal level at a distance $\frac{\sqrt{3}l}{2}$ from point $A$. At the lowest point bob hits a block of identical mass $m$ elastically. The maximum compression in the spring is $2C$ meter. Find the value of $C$.

(take $\frac{ml}{k}=\frac{56}{10} \mathrm{kg}-{\mathrm{m}}^2 {\mathrm{N}}^{-1}$, $g=10 \mathrm{m} {\mathrm{s}}^{-2}$ and ground is smooth)

A ball is dropped from height $H$. After striking the ground $n^{\text{th }}$ time it rebounds to height $h$. Then coefficient of restitution is